
2023.11.15 タイトルを修正しました。
「答えを覚えると計算がラクになる」という話です。
すぐに分かる足し算と、分からない足し算の違い
さっそくですが、以下の足し算の答えはすぐ分かりますか?
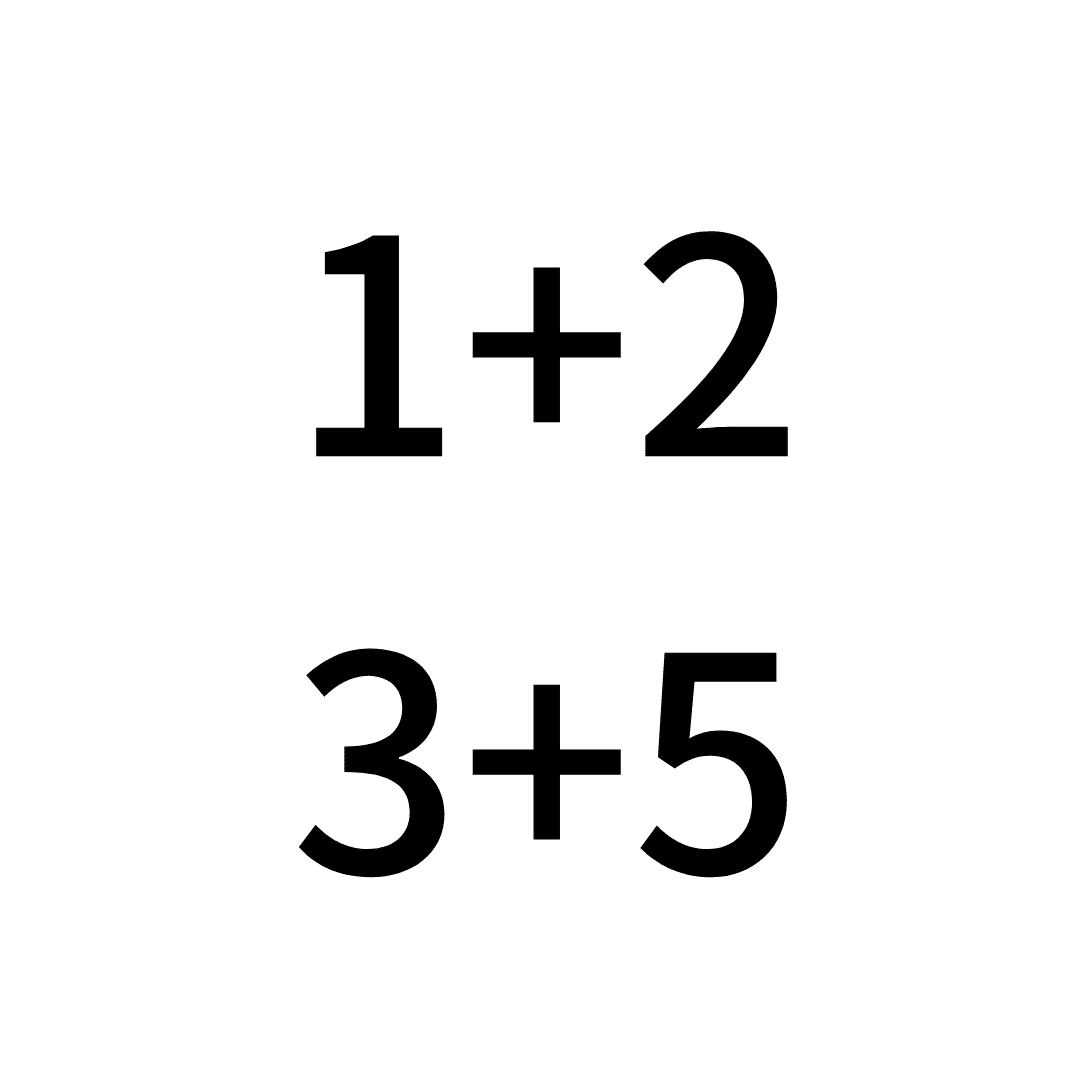
すぐに、3だ!8だ!と答えが出たのではないでしょうか。
では、これはどうでしょうか。
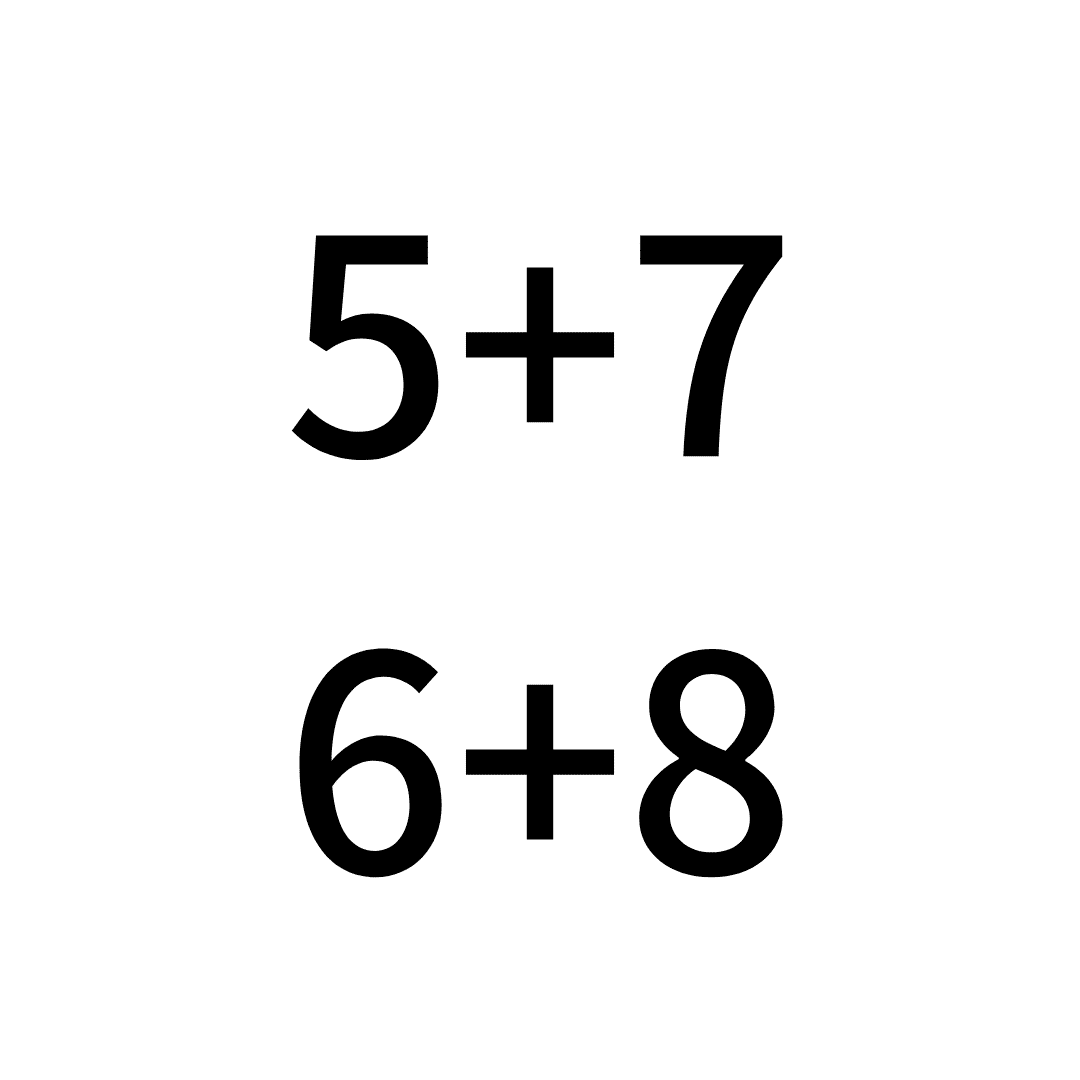
すぐに答えがわかった、という人が多いのかなと思います、が…
少し考えて答えを出した人もいると思います。
では、なぜ少し考える必要があるのでしょうか?
それは、5+7や6+8などの足し算は、1+2や3+5などと違って、繰り上がりのある足し算だからです。
足し算の理屈が分かる、しかし手間はかかる「さくらんぼ」計算
少し考えて答えを出した人は、おそらく頭の中で以下のような過程をたどったのではないでしょうか?
5+7を例にすると…

いわゆる「さくらんぼ」式の計算方法です。(数を分解したときのイメージが、さくらんぼに似ているため)
まず、10のかたまりを作ってから、残りの数を足す。
小学校の算数の授業で、繰り上がりのある足し算の方法を、
だいたいこのように教わるのではないでしょうか(さくらんぼ、という名前は出ないとしても)。
これは確かに計算の仕組みを説明するものとして、よく分かりますし、マスターしておくべきです。
ただ、原理は原理。
そして、とくに実生活の場面では、何より手間がかかる。
分解してあとで足すほうの数字を忘れてしまった…なんてこともあり得ます。
理解するための原理と、処理するための技術は、今回ちょっと分けましょう。
今回の足し算の場合、
覚えたほうがが早く答えが出るのです。
足し算の組み合わせは限られている
一けたの足し算の組み合わせは、これだけあります。

45パターン
このうち、「1+~」と「~+9」のパターンは、機械的に処理できるので分かりやすく、抵抗が少ないかなと思います。

また、足して10になるパターンも、覚えていると思います。
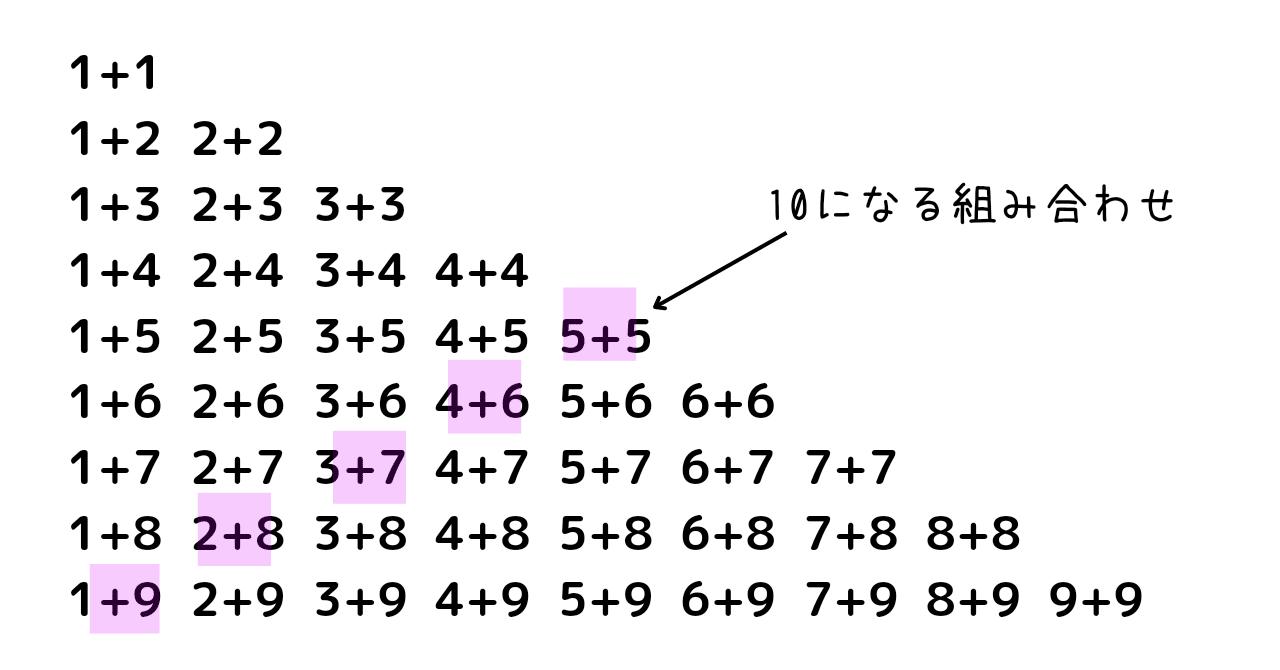
「2+2」や「6+6」など、同じ数を足すパターンも、九九からの連想で覚えているのではないでしょうか。
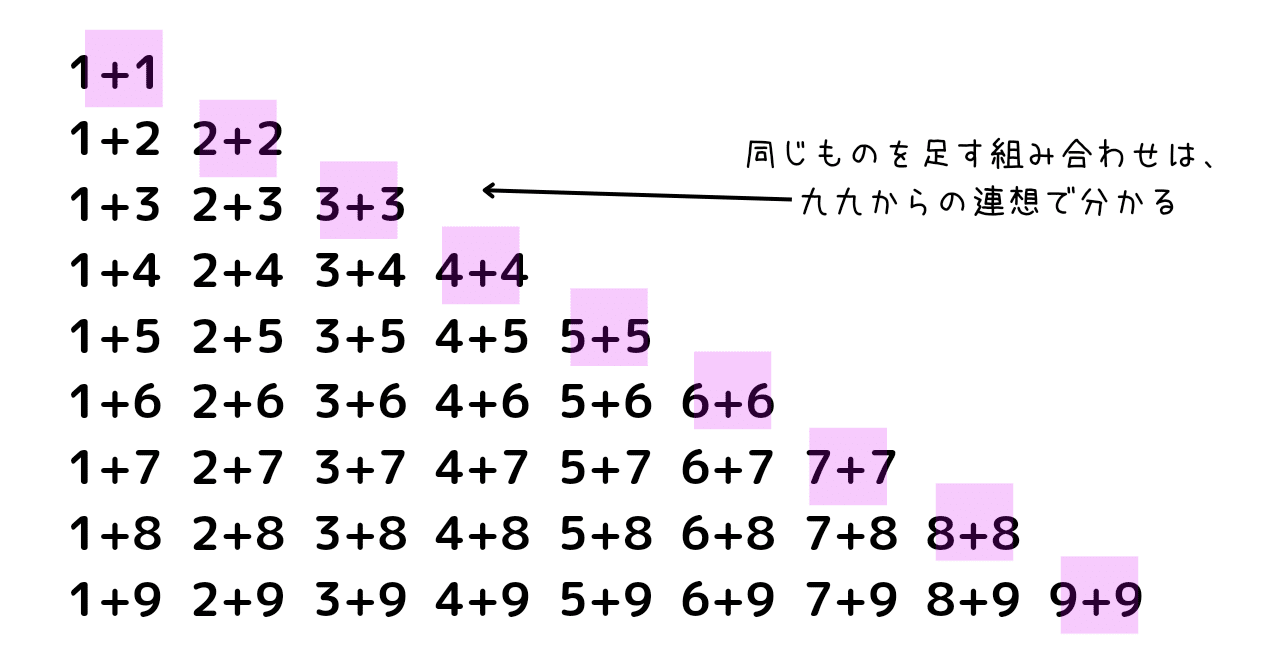
ということは、だいたい、45パターンのうち27パターン程度は抵抗なく足し算できるということです。

では、以下、黄色にした部分、「2+3」や「4+5」のパターンはどうでしょうか。
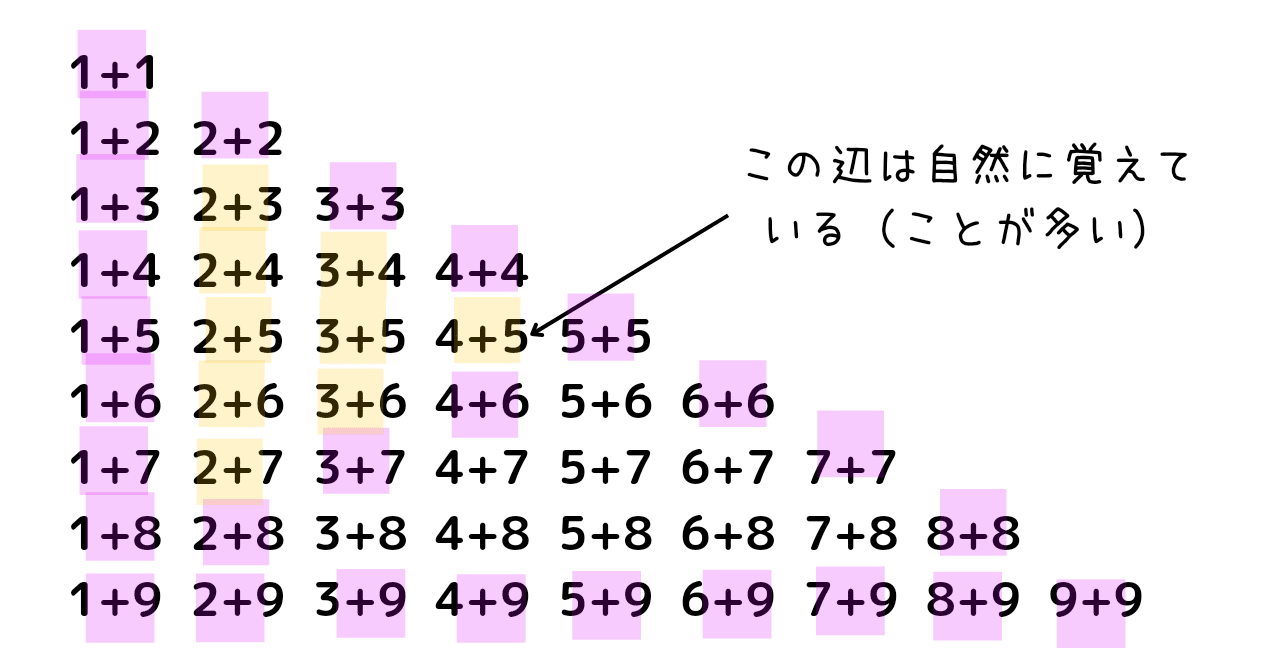
この辺りは、規則的に処理できるわけではないものですが、
繰り上がりの手間がないので、
「あ、この組み合わせの答えはコレだな」と、
なんとなく覚えてしまっているのではないでしょうか。
それでは、以下の青色にした部分、「5+8」や「7+8」のパターンはどうでしょう。
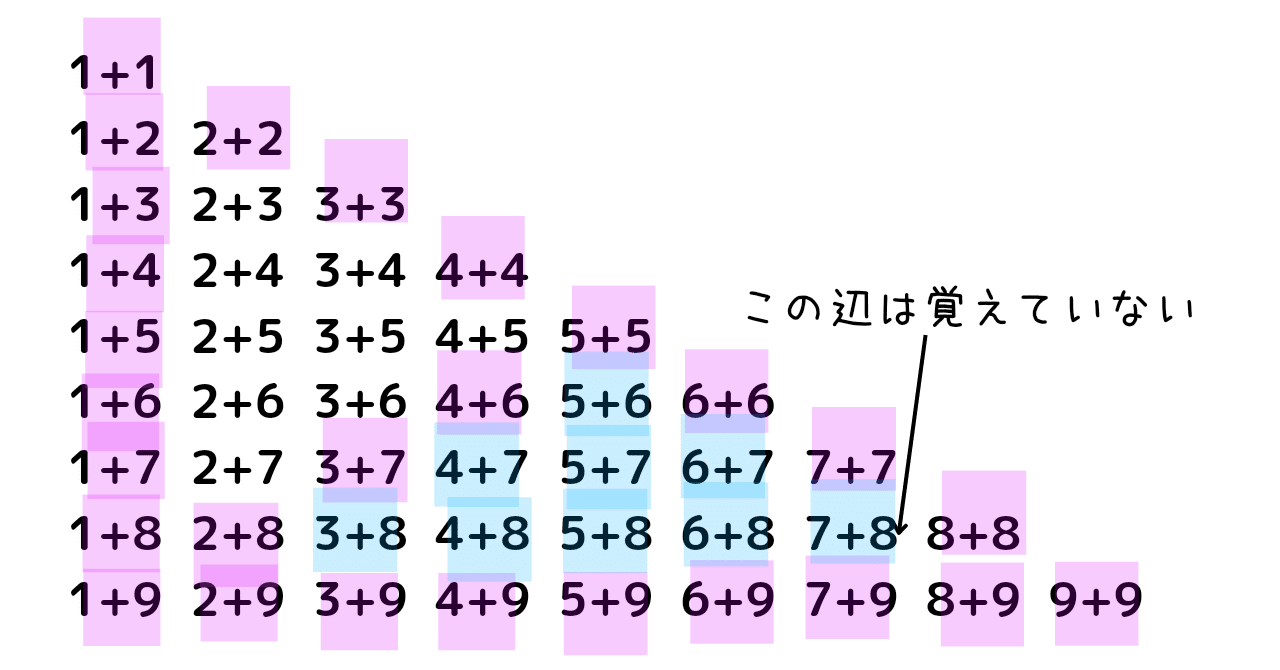
もちろん人によりますが、
ここは、さきほどの「さくらんぼ」式で段階を踏んで答えを出している、
という人もいると思います。
でも、
これだけ覚えてしまってるのなら、いっそのこと、この部分も覚えてしまってもいいと思いませんか?
何もこの部分だけを、理屈のとおり律儀にやる必要はないわけです。
これらのパターンも、覚えてしまおう
視覚的に覚えられるように、青色にした部分を、答えの数ごとにピックアップしたものを載せていきます。
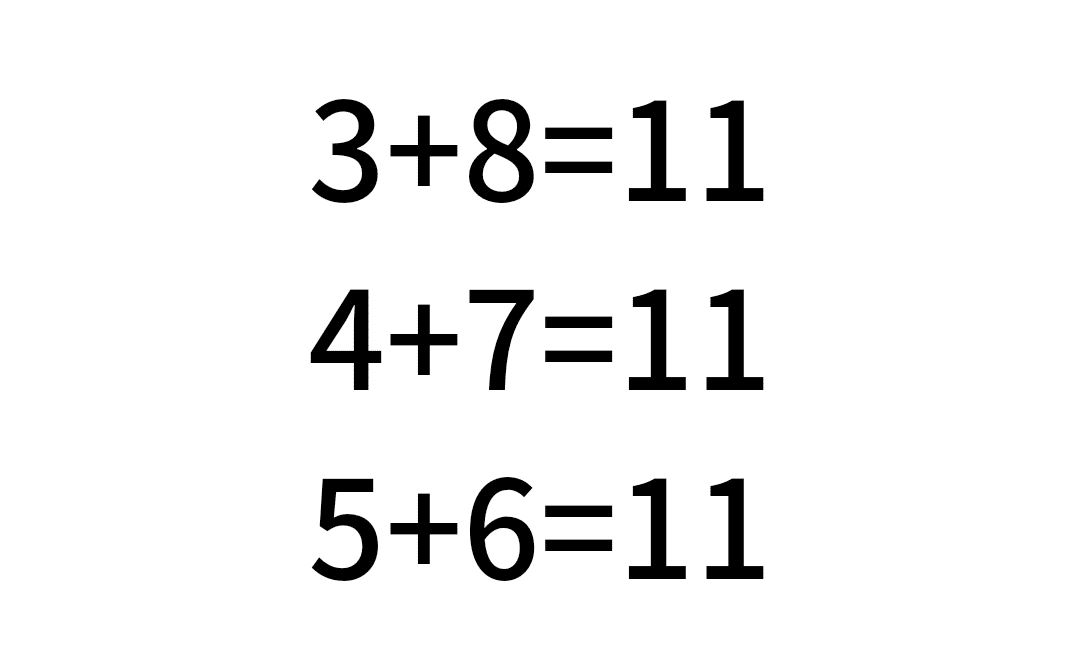
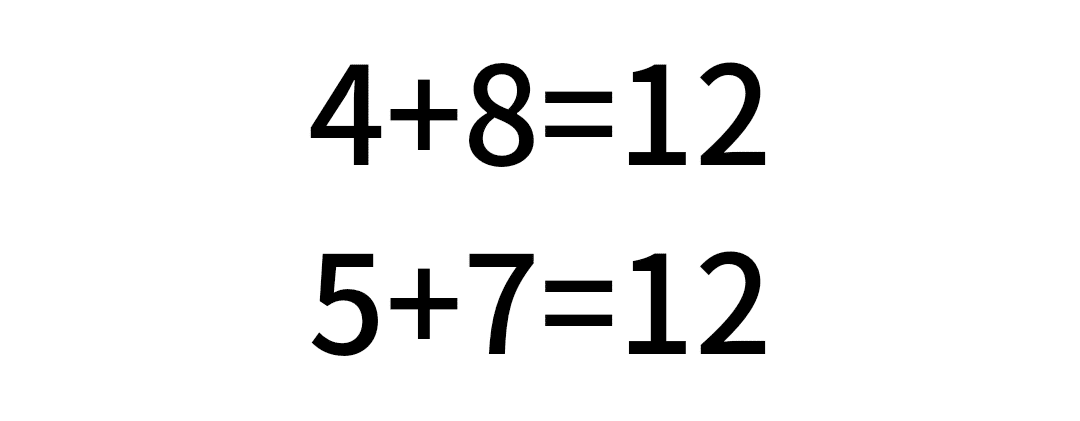
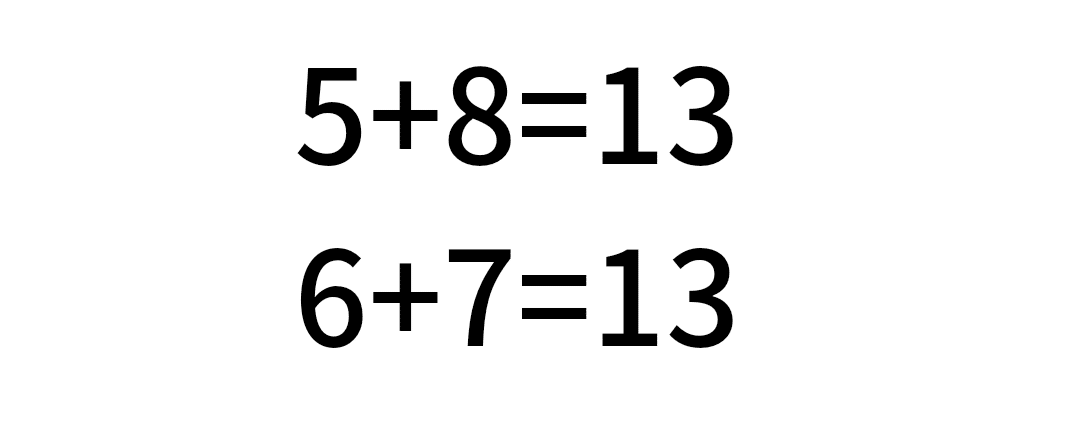
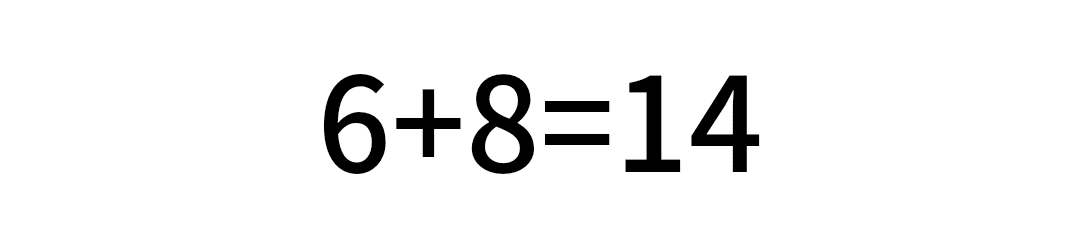
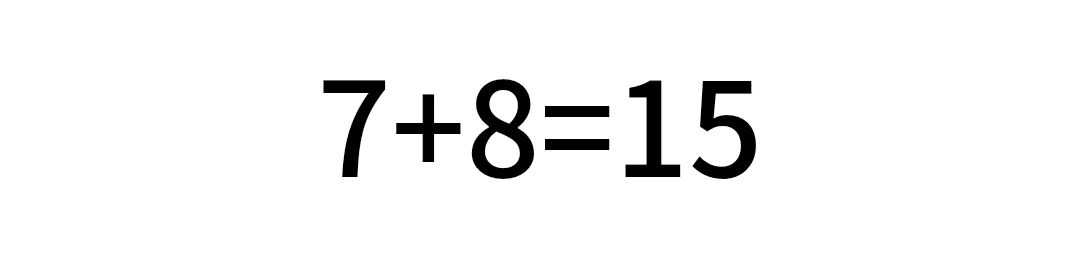
桁が多かったり、組み合わせ無限の足し算。
でも、基本はこれらのパターンの組み合わせなのです。
理屈を覚えているのなら、覚えて、反射的に答えを思い浮かべられるようにすればOK!
計算するときの負担がグッと減りますよ。
いままで律儀に処理していた人、ぜひやってみてください!




コメント